உள்ளடக்கம்

• படிகள்
• பகுதி 1 ல் 2: அடிப்படைகள்
• பகுதி 2 இன் 2: SLAE களைத் தீர்க்க மேட்ரிக்ஸ் உருமாற்றம்
• குறிப்புகள்

சமன்பாடுகளின் அமைப்பு என்பது இரண்டு அல்லது அதற்கு மேற்பட்ட சமன்பாடுகளின் தொகுப்பாகும், இது பொதுவான அறியப்படாத தொகுப்பைக் கொண்டுள்ளது, எனவே, ஒரு பொதுவான தீர்வு. நேரியல் சமன்பாடுகளின் அமைப்பின் வரைபடம் இரண்டு நேர் கோடுகள், மற்றும் அமைப்புக்கான தீர்வு இந்த நேர்கோடுகளின் குறுக்குவெட்டு ஆகும். நேரியல் சமன்பாடுகளின் இத்தகைய அமைப்புகளைத் தீர்க்க, மெட்ரிஸ்களைப் பயன்படுத்துவது பயனுள்ளது மற்றும் வசதியானது.

படிகள்

பகுதி 1 ல் 2: அடிப்படைகள்

1. 1 கலைச்சொல். நேரியல் சமன்பாடுகளின் அமைப்புகள் பல்வேறு கூறுகளால் ஆனவை. ஒரு மாறி என்பது அகரவரிசை எழுத்தால் குறிக்கப்படுகிறது (பொதுவாக x அல்லது y) மற்றும் உங்களுக்கு இன்னும் தெரியாத மற்றும் கண்டுபிடிக்க வேண்டிய எண்ணைக் குறிக்கிறது. மாறிலி என்பது ஒரு குறிப்பிட்ட எண்ணாகும், அது அதன் மதிப்பை மாற்றாது.குணகம் என்பது மாறியின் முன்னால் உள்ள எண், அதாவது, மாறி பெருக்கப்படும் எண்.
   • உதாரணமாக, ஒரு நேரியல் சமன்பாட்டிற்கு, 2x + 4y = 8, x மற்றும் y மாறிகள், 8 நிலையானது, மற்றும் எண்கள் 2 மற்றும் 4 ஆகியவை குணகங்களாகும்.
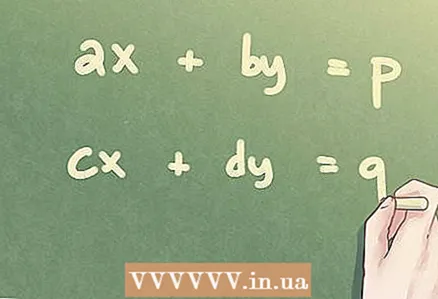2. 2 நேரியல் சமன்பாடுகளின் அமைப்பு. இரண்டு மாறிகள் கொண்ட நேரியல் இயற்கணித சமன்பாடுகளின் அமைப்பு (SLAE) பின்வருமாறு எழுதப்படலாம்: ax + by = p, cx + dy = q. எந்த மாறிலிகளும் (p, q) பூஜ்ஜியமாக இருக்கலாம், ஆனால் ஒவ்வொரு சமன்பாடுகளும் குறைந்தது ஒரு மாறியை (x, y) கொண்டிருக்க வேண்டும்.
3. 3 மேட்ரிக்ஸ் வெளிப்பாடுகள். எந்த ஸ்லேவையும் மேட்ரிக்ஸ் வடிவத்தில் எழுதலாம், பின்னர், மெட்ரிக்ஸின் இயற்கணித பண்புகளைப் பயன்படுத்தி அதைத் தீர்க்கவும். மேட்ரிக்ஸ் வடிவத்தில் சமன்பாடுகளின் அமைப்பை எழுதும் போது, ​​A ஆனது மேட்ரிக்ஸின் குணகங்களையும், C ஆனது நிலையான மெட்ரிக்ஸையும், X என்பது தெரியாத மேட்ரிக்ஸையும் குறிக்கிறது.
   • எடுத்துக்காட்டாக, மேலே உள்ள SLAE ஐ பின்வரும் மேட்ரிக்ஸ் வடிவத்தில் மீண்டும் எழுதலாம்: A x X = C.
4. 4 விரிவாக்கப்பட்ட அணி இலவச விதிமுறைகளின் (மாறிலிகள்) மேட்ரிக்ஸை இடது பக்கத்திற்கு மாற்றுவதன் மூலம் நீட்டிக்கப்பட்ட அணி பெறப்படுகிறது. உங்களிடம் A மற்றும் C ஆகிய இரண்டு மெட்ரிக்ஸ் இருந்தால், விரிவாக்கப்பட்ட அணி இப்படி இருக்கும்:
   • எடுத்துக்காட்டாக, பின்வரும் நேரியல் சமன்பாடுகளின் அமைப்புக்கு:
     2x + 4y = 8
     x + y = 2
     விரிவாக்கப்பட்ட அணி 2x3 ஆக இருக்கும் மற்றும் இப்படி இருக்கும்:

பகுதி 2 இன் 2: SLAE களைத் தீர்க்க மேட்ரிக்ஸ் உருமாற்றம்

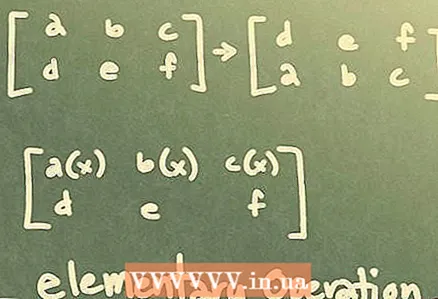1. 1 ஆரம்ப செயல்பாடுகள். நீங்கள் ஒரு மேட்ரிக்ஸில் சில செயல்பாடுகளைச் செய்யலாம், இதனால் அசல் ஒன்றிற்கு சமமான மேட்ரிக்ஸ் கிடைக்கும். இத்தகைய செயல்பாடுகள் ஆரம்பநிலை என்று அழைக்கப்படுகின்றன. எடுத்துக்காட்டாக, 2x3 மேட்ரிக்ஸைத் தீர்க்க, மேட்ரிக்ஸை முக்கோண வடிவத்திற்கு கொண்டு வர வரிசை செயல்பாடுகளைச் செய்ய வேண்டும். இத்தகைய செயல்பாடுகள் இருக்கலாம்:
   • இரண்டு வரிகளின் வரிசைமாற்றம்.
   • ஒரு சரத்தை ஒரு nonzero எண்ணால் பெருக்குதல்.
   • ஒரு சரத்தை பெருக்கி அதை இன்னொருவரிடம் சேர்ப்பது.
2. 2 இரண்டாவது வரியை ஒரு நொன்ஜெரோ எண்ணால் பெருக்கல். நீங்கள் இரண்டாவது வரியில் பூஜ்ஜியத்தை விரும்பினால், அதை சாத்தியமாக்க நீங்கள் வரியை பெருக்கலாம்.
   • உதாரணமாக, உங்களிடம் இது போன்ற மேட்ரிக்ஸ் இருந்தால்:
     
     
     நீங்கள் முதல் வரியை வைத்து இரண்டாவது வரியில் பூஜ்ஜியத்தைப் பெற அதைப் பயன்படுத்தலாம். இதைச் செய்ய, நீங்கள் முதலில் இரண்டாவது வரியை 2 ஆல் பெருக்க வேண்டும்:
3. 3 மீண்டும் பெருக்கவும். முதல் வரிசையில் பூஜ்ஜியத்தைப் பெற, இதேபோன்ற கையாளுதல்களைப் பயன்படுத்தி நீங்கள் மீண்டும் பெருக்க வேண்டியிருக்கும்.
   • மேலே உள்ள எடுத்துக்காட்டில், நீங்கள் இரண்டாவது வரியை -1 ஆல் பெருக்க வேண்டும்:
     
     
     பெருக்கத்திற்குப் பிறகு, மேட்ரிக்ஸ் இப்படி இருக்கும்:
4. 4 முதல் வரியை இரண்டாவது வரிசையில் சேர்க்கவும். முதல் நெடுவரிசை மற்றும் இரண்டாவது வரிசையின் இடத்தில் பூஜ்ஜியத்தைப் பெற வரிசைகளைச் சேர்க்கவும்.
   • எங்கள் எடுத்துக்காட்டில், பின்வரும் வரிகளைப் பெற இரண்டு வரிகளையும் சேர்க்கவும்:
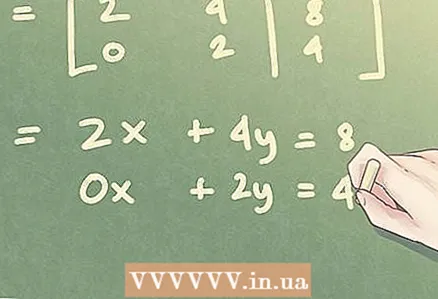5. 5 ஒரு முக்கோண மேட்ரிக்ஸிற்கான நேரியல் சமன்பாடுகளின் புதிய அமைப்பை எழுதுங்கள். நீங்கள் முக்கோண மேட்ரிக்ஸைப் பெற்றவுடன், நீங்கள் மீண்டும் SLAE க்குச் செல்லலாம். மேட்ரிக்ஸின் முதல் நெடுவரிசை தெரியாத மாறி x க்கு ஒத்திருக்கிறது, இரண்டாவது தெரியாத மாறி y க்கு ஒத்திருக்கிறது. மூன்றாவது நெடுவரிசை சமன்பாட்டின் குறுக்கீட்டை ஒத்துள்ளது.
   • எங்கள் உதாரணத்திற்கு, நேரியல் சமன்பாடுகளின் புதிய அமைப்பு வடிவத்தை எடுக்கும்:
6. 6 மாறிகளில் ஒன்றிற்கான சமன்பாட்டைத் தீர்க்கவும். புதிய SLAE இல், எந்த மாறி மாறி சமன்பாட்டைக் கண்டறிந்து தீர்க்க எளிதானது என்பதைத் தீர்மானிக்கவும்.
   • எங்கள் எடுத்துக்காட்டில், முடிவிலிருந்து தீர்க்க மிகவும் வசதியானது, அதாவது கடைசி சமன்பாட்டிலிருந்து முதல் வரை, கீழே இருந்து மேலே நகரும். இரண்டாவது சமன்பாட்டிலிருந்து, y க்கு ஒரு தீர்வை நாம் எளிதாகக் காணலாம், ஏனெனில் நாங்கள் x ஐ விட்டோம், அதனால் y = 2.
7. 7 மாற்று முறை மூலம் தெரியாத இரண்டாவது கண்டுபிடிக்கவும். மாறிகளில் ஒன்றை நீங்கள் கண்டறிந்தவுடன், இரண்டாவது மாறியைக் கண்டுபிடிக்க அதை இரண்டாவது சமன்பாட்டில் செருகலாம்.
   • எங்கள் எடுத்துக்காட்டில், தெரியாத x ஐக் கண்டுபிடிக்க y ஐ முதல் சமன்பாட்டில் 2 உடன் மாற்றவும்:

குறிப்புகள்

• மேட்ரிக்ஸ் கூறுகள் பொதுவாக ஸ்கேலர்கள் என குறிப்பிடப்படுகின்றன.
• 2x3 மேட்ரிக்ஸைத் தீர்க்க, நீங்கள் அடிப்படை வரிசை செயல்பாடுகளைச் செய்ய வேண்டும். நெடுவரிசைகளில் இந்த செயல்பாடுகளை நீங்கள் செய்ய முடியாது.